הבעיה הראשית של דינמיקה
בעיות רבות מתחומים כמו אסטרונימיה, תחבורה, ארטילריה וכדומה, מנוסחות באופן הבא: קיים גוף, אליו אפשר להתייחס כאל מסה נקודתית (למשל, כוכב לכת, פגז, טיל וכו'); ידועים כוחות, הפועלים על גוף זה. יש למצוא חוק לתנועה של נקודה זו, כלומר לבטא את הקואורדינטות שלה כפונקציות של זמן. כך מנוסחת הבעיה העיקרית של דינמיקה, והניסוח היותר קצר שלה הוא כדלקמן: למצוא חוק תנועה של מסה נקודתית, אם ידועים כוחות הפועלים עליה.
על מנת לפתור את הבעיה, קודם כל מוצאים תאוצה שיש למסה נקודתית באמצעות החוק הראשי של דינמיקה (החוק השני של ניוטון). לאחר מכן, באמצעות נוסחאות ידועות מקינמטיקה מוצאים ביטויים המתארים מהירויות וקואורדינטות רצוייות.
באופן כללי, קשיים מתמטיים המופיעים בפתרון הבעיה עלולים להיות משמעותיים. אולם יחד עם זאת, הפתרון הפרטי של כל בעיה יכול להתקבל באמצעות חישובים מספריים - בקירוב שמספיק לפותר הבעיה.
אנו נדון בכמה בעיות פשוטות בהמשך. באמצעות הדוגמאות הללו נוכל להבין מה צריך בכדי לפתור את הבעיה הראשית של דינמיקה.
את הפתרון המדוייק אנו נקבל אך ורק במקרה הפשוט - כאשר נדון במקרה בו הגוף נע תחת השפעה של כוח קבוע.
תנועה של מסה נקודתית תחת השפעה של כוח הכובד
נניח כי על מסה נקודתית הנמצאת בתנועה, לא פועלים שום כוחות מלבד כוח הכובד. תרחיש כזה אפשרי, למשל, על הירח ששם אין אטמוספרה. אולם, בקירוב טוב מצב כזה אפשרי גם על פני כדור הארץ, אם מהירות המסה הנקדותית לא עולה על כמה מטרים לשנייה, כי במהירויות כאלו ניתן להזניח את התנגדות האוויר.
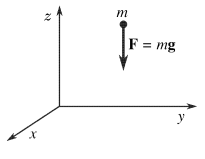אנו נניח כי מערכת הייחוס הצמודה אל כדור הארץ היא אינרציאלית. נבחר את הצירים כמתואר באיור. נבטא את הכוח הפועל על המסה הנקודתית בצורה הבאה:
$$\mathbf{F}=\mathbf{P}=m\mathbf{g} \tag{1}$$
ואם נפרק לרכיבים
$$F_x=0,~~F_y=0,~~F_z=-mg \tag{2}$$
החוק הראשי של דינמיקה ייראה כך
$$F_x=ma_x=0,~~F_y=ma_y=0,~~F_z=ma_z=-mg \tag{3}$$
לפיכך, רכיבי התאוצה על הצירים
$$a_x=0,~~a_y=0,~~a_z=-g \tag{4}$$
כעת, אין זאת בעיה למצוא את חוק התנועה. לאורך ציר האַבּסצִיסָה (כך נקרא ציר $x$), הנקודה נעה ללא תאוצה, כלומר בתנועה קצובה. במקרה כזה מהירות הנקודה נשארת קבועה, והקואורדינטה שלה - פונקציה לינארית של זמן:
$$v_x=u_0=\text{const},~~~x=x_0+u_0t \tag{5}$$
באופן דומה עבור ציר אוֹרדִינָטָה (כך נקרא ציר $y$)
$$v_y=w_0=\text{const},~~~y=y_0+w_0t \tag{6}$$
ולבסוף, לאורך ציר האפליקטה (ציר $z$) הנקודה נעה בתאוצה קבועה. לכן המהירות שלה הינה פונקציה לינארית של זמן, והקואורדינטה שלה - פונקציה ריבועית של זמן:
$$v_z=v_0+a_zt=v_0-gt,\\z=z_0+v_0t+\frac{a_z t^2}{2}=z_0+v_0 t -\frac{g t^2}{2} \tag{7}$$
אם כן, מצאנו את החוקיות של התנועה. היא נראית כך
$$x=x_0+u_0t,~~y=y_0+w_0t,~~z=z_0+v_0t-\frac{g t^2}{2}\tag{8}$$
בביטוי של חוק התנועה מופיעים שישה קבועים שרירותיים: קואורדינטות התחלתיות $x_0, y_0, z_0$ ומהירויות התחלתיות $u_0, w_0, v_0$. הם קובעים את המיקום ואת המהירות של המסה הנקודתית בנקודת זמן $t=0$, שאנו קובעים בתור נקודת זמן התחלתית.
מערכת משוואות (5)-(8) מתארת את כל המקרים האפשריים של תנועה של מסה נקודתית תחת השפעה של כוח הכובד. על מנת לקבל מקרה פרטי כלשהו, יש לרשום את התנאים ההתחלתיים הספציפיים.
כך לדוגמה ניתן לנתח תנועה בליסטית. נניח כי מסה נקודתית נזרקת מראשית הצירים במהירות $\mathbf{V_0}$ בזווית $\alpha$ עם האופק, ווקטור המהירות ההתחלתית נמצא על מישור $yz$ כמתואר באיור הבא
התנאים ההתחלתיים הם
$$V_{0,x}=w_0=0,~~~V_{0,y}=u_0=V_0\cos \alpha,~~~V_{0,z}=v_0=V_0 \sin \alpha \tag{9}$$
חוק התנועה נראה כך:
$$x=0,~~~y=V_0 t \cos \alpha,~~~z=V_0 t \sin \alpha - \frac{g t^2}{2} \tag{10}$$
נראה כעת כי הנקודה נעה במסלול פרבולי הנמצא על המישור האנכי. מ-(10) נובע: $t=\frac{y}{V_0 \cos \alpha}$. אם נציב ערך זה של $t$ במשוואה השלישית, נקבל
$$z=y \tan \alpha - \frac{g y^2}{2 V_0^2 \cos^2 \alpha} \tag{11}$$
וזה אכן משוואת פרבולה באופן כללי. את טווח הזריקה אנו נקבל אם נציב ב-(11) $z=0, y=L$; ואז
$$L=\frac{2 V_0^2 \tan \alpha \cos^2 \alpha}{g}=\frac{V_0 ^2 \sin 2\alpha}{g} \tag{12}$$
במאמר על תנועה בליסטית כבר הזכרנו כי הטווח יהיה מקסימלי אם זווית הזריקה תיהיה בת $45^{\circ}$. כעת אנו רואים כי זה מאומת גם על ידי ביטוי טריגונומטרי, הרי כאשר $\alpha=45^{\circ}$ הביטוי עם סינוס מקבל את הערך המקסימלי 1 ($\sin 2 \alpha = \sin 90^{\circ}=1$).
גדלים, הקובעים את חוק התנועה של מסה נקדותית
בדוגמת התרגילים לעיל, ראינו כי על מנת לקבוע את חוק התנועה של מסה נקודתית יש צורך בנתונים הבאים:
על מנת לפתור את הבעיה, קודם כל מוצאים תאוצה שיש למסה נקודתית באמצעות החוק הראשי של דינמיקה (החוק השני של ניוטון). לאחר מכן, באמצעות נוסחאות ידועות מקינמטיקה מוצאים ביטויים המתארים מהירויות וקואורדינטות רצוייות.
באופן כללי, קשיים מתמטיים המופיעים בפתרון הבעיה עלולים להיות משמעותיים. אולם יחד עם זאת, הפתרון הפרטי של כל בעיה יכול להתקבל באמצעות חישובים מספריים - בקירוב שמספיק לפותר הבעיה.
אנו נדון בכמה בעיות פשוטות בהמשך. באמצעות הדוגמאות הללו נוכל להבין מה צריך בכדי לפתור את הבעיה הראשית של דינמיקה.
את הפתרון המדוייק אנו נקבל אך ורק במקרה הפשוט - כאשר נדון במקרה בו הגוף נע תחת השפעה של כוח קבוע.
תנועה של מסה נקודתית תחת השפעה של כוח הכובד
נניח כי על מסה נקודתית הנמצאת בתנועה, לא פועלים שום כוחות מלבד כוח הכובד. תרחיש כזה אפשרי, למשל, על הירח ששם אין אטמוספרה. אולם, בקירוב טוב מצב כזה אפשרי גם על פני כדור הארץ, אם מהירות המסה הנקדותית לא עולה על כמה מטרים לשנייה, כי במהירויות כאלו ניתן להזניח את התנגדות האוויר.
$$\mathbf{F}=\mathbf{P}=m\mathbf{g} \tag{1}$$
ואם נפרק לרכיבים
$$F_x=0,~~F_y=0,~~F_z=-mg \tag{2}$$
החוק הראשי של דינמיקה ייראה כך
$$F_x=ma_x=0,~~F_y=ma_y=0,~~F_z=ma_z=-mg \tag{3}$$
לפיכך, רכיבי התאוצה על הצירים
$$a_x=0,~~a_y=0,~~a_z=-g \tag{4}$$
כעת, אין זאת בעיה למצוא את חוק התנועה. לאורך ציר האַבּסצִיסָה (כך נקרא ציר $x$), הנקודה נעה ללא תאוצה, כלומר בתנועה קצובה. במקרה כזה מהירות הנקודה נשארת קבועה, והקואורדינטה שלה - פונקציה לינארית של זמן:
$$v_x=u_0=\text{const},~~~x=x_0+u_0t \tag{5}$$
באופן דומה עבור ציר אוֹרדִינָטָה (כך נקרא ציר $y$)
$$v_y=w_0=\text{const},~~~y=y_0+w_0t \tag{6}$$
ולבסוף, לאורך ציר האפליקטה (ציר $z$) הנקודה נעה בתאוצה קבועה. לכן המהירות שלה הינה פונקציה לינארית של זמן, והקואורדינטה שלה - פונקציה ריבועית של זמן:
$$v_z=v_0+a_zt=v_0-gt,\\z=z_0+v_0t+\frac{a_z t^2}{2}=z_0+v_0 t -\frac{g t^2}{2} \tag{7}$$
אם כן, מצאנו את החוקיות של התנועה. היא נראית כך
$$x=x_0+u_0t,~~y=y_0+w_0t,~~z=z_0+v_0t-\frac{g t^2}{2}\tag{8}$$
בביטוי של חוק התנועה מופיעים שישה קבועים שרירותיים: קואורדינטות התחלתיות $x_0, y_0, z_0$ ומהירויות התחלתיות $u_0, w_0, v_0$. הם קובעים את המיקום ואת המהירות של המסה הנקודתית בנקודת זמן $t=0$, שאנו קובעים בתור נקודת זמן התחלתית.
מערכת משוואות (5)-(8) מתארת את כל המקרים האפשריים של תנועה של מסה נקודתית תחת השפעה של כוח הכובד. על מנת לקבל מקרה פרטי כלשהו, יש לרשום את התנאים ההתחלתיים הספציפיים.
כך לדוגמה ניתן לנתח תנועה בליסטית. נניח כי מסה נקודתית נזרקת מראשית הצירים במהירות $\mathbf{V_0}$ בזווית $\alpha$ עם האופק, ווקטור המהירות ההתחלתית נמצא על מישור $yz$ כמתואר באיור הבא
התנאים ההתחלתיים הם
$$V_{0,x}=w_0=0,~~~V_{0,y}=u_0=V_0\cos \alpha,~~~V_{0,z}=v_0=V_0 \sin \alpha \tag{9}$$
חוק התנועה נראה כך:
$$x=0,~~~y=V_0 t \cos \alpha,~~~z=V_0 t \sin \alpha - \frac{g t^2}{2} \tag{10}$$
נראה כעת כי הנקודה נעה במסלול פרבולי הנמצא על המישור האנכי. מ-(10) נובע: $t=\frac{y}{V_0 \cos \alpha}$. אם נציב ערך זה של $t$ במשוואה השלישית, נקבל
$$z=y \tan \alpha - \frac{g y^2}{2 V_0^2 \cos^2 \alpha} \tag{11}$$
וזה אכן משוואת פרבולה באופן כללי. את טווח הזריקה אנו נקבל אם נציב ב-(11) $z=0, y=L$; ואז
$$L=\frac{2 V_0^2 \tan \alpha \cos^2 \alpha}{g}=\frac{V_0 ^2 \sin 2\alpha}{g} \tag{12}$$
במאמר על תנועה בליסטית כבר הזכרנו כי הטווח יהיה מקסימלי אם זווית הזריקה תיהיה בת $45^{\circ}$. כעת אנו רואים כי זה מאומת גם על ידי ביטוי טריגונומטרי, הרי כאשר $\alpha=45^{\circ}$ הביטוי עם סינוס מקבל את הערך המקסימלי 1 ($\sin 2 \alpha = \sin 90^{\circ}=1$).
גדלים, הקובעים את חוק התנועה של מסה נקדותית
בדוגמת התרגילים לעיל, ראינו כי על מנת לקבוע את חוק התנועה של מסה נקודתית יש צורך בנתונים הבאים:
- יש לדעת את הכוח שפועל על המסה, אשר מוגדר בתור פונקציה של זמן או של קואורדינטה;
- יש לדעת את התנאים ההתחלתיים: קואורדינטות ומהירות של המסה בנקודת זמן כלשהי (במקום המהירות ההתחלתית יכול להיות נתון התנע ההתחלתי $\mathbf{p_0}=m\mathbf{v_0}$.)
כך למשל, אם אנו יודעים את כוחות האינטראקציה הפועלים בין השמש לבין כוכבי הלכת הסובבים אותה, ואת הקואורדינטות והמהירויות של כוכבי הלכת בנקודת זמן כלשהי (כלומר, התנאים ההתחלתיים), ניתן לגלות את התנועה שהייתה להם לפני הרבה שנים, וגם לחזות את התנועה העתידית שלהם. בפרט, ניתן לחזות תופעות כמו ליקוי חמה או ירח.
אם ידועה המהירות והקואורדינטה של חללית בנקודת זמן כלשהי, וידועים הכוחות הפועלים עליה, ניתן לחשב את מסלולה; לחשב היכן היא תימצא בכל נקודת זמן; כך גם ניתן לחזות את הקואורדינטות של נקודת הנחיתה העתידית.
אם כן, בדוגמת כמה תרגילים פשוטים ממכניקה ניוטונית, הבנו כי כוח ונתונים התחלתיים קובעים לגמרי את חוק התנועה של מסה נקודתית.
עם התפתחות המדע, הסתבר כי בעולם החלקיקים הזעירים לא ניתן לקבוע נתונים התחלתיים כמו במכניקה ניוטונית (נדון בכך במאמרים יותר מתקדמים בהמשך).
אין תגובות:
הוסף רשומת תגובה